4.1 The logic of hypothesis testing

Central to all statistical testing is the underlying logic of hypothesis testing. All of the statistical tests that we cover in this module are built on this logic - and so it marks a great place for us to start our venture into inferential statistics.

4.1.1 Revisiting the hypotheses

In Module 4 on Canvas, you will have had the chance to write your own hypothesis. This hypothesis guides the overall research and methodological design of our studies. However, you may have noticed that the hypotheses discussed in the video are not quite in the same format. This is because ‘hypothesis’ in this context refers to statistical hypotheses.

Statistical hypotheses are formal statements that we use when testing for an effect. As mentioned in the video above, we propose two contrasting hypotheses when we want to do statistical testing:

• The null hypothesis (\(H_0\)) - that there is no effect or difference
• The alternative hypothesis (\(H_1\)) - that there is an effect or difference

We can never know for sure whether one hypothesis is correct over the other. Instead, we choose to either reject or not reject the null hypothesis.

4.1.2 The issue of tails

There are two main types of alternative hypotheses:

• Two-tailed: we hypothesise that something is happening regardless of whether it’s greater, smaller, increasing, decreasing etc…
• One-tailed: we hypothesise that the effect has a direction

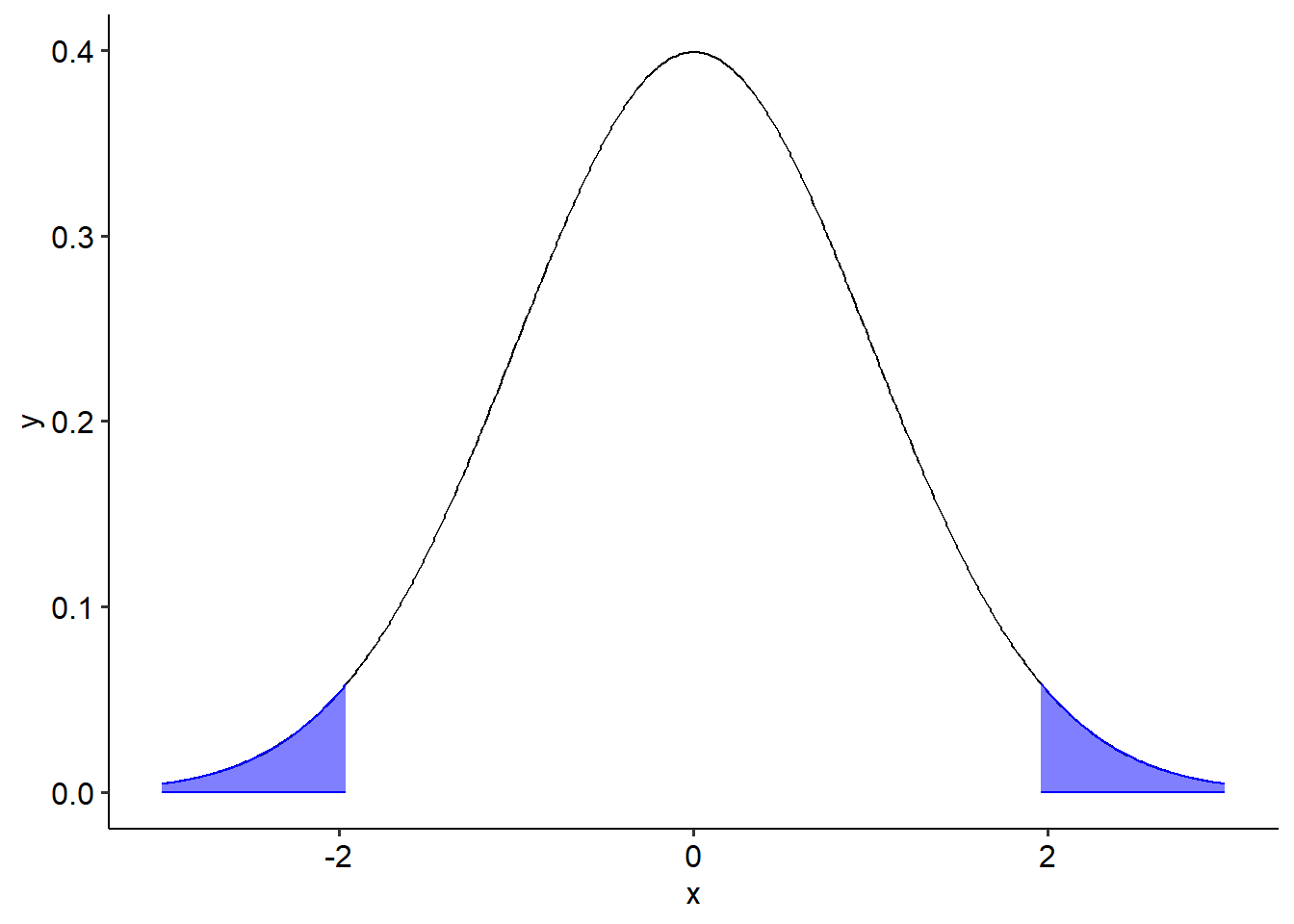
In a two-tailed hypothesis, we predict that an effect is occuring but we don’t predict anything beyond that. For example, if we are comparing whether two groups are different our alternative hypothesis would be that they are different - but we don’t predict whether group A will be bigger than group B or vice versa. These are sometimes called non-directional hypotheses.

The blue areas on the curve on the right represent a 0.05 level of signifiance for a two-tailed hypothesis test. This is essentially how likely it is that we would observe our effect/difference if nothing was happening. If a difference is large enough that it falls within these blue tails, it is statistically significant. This is because if nothing really was happening, it would be unlikely that we see an effect/difference this big. Therefore, we would choose to reject the null hypothesis at this would fall below our chosen significance level.

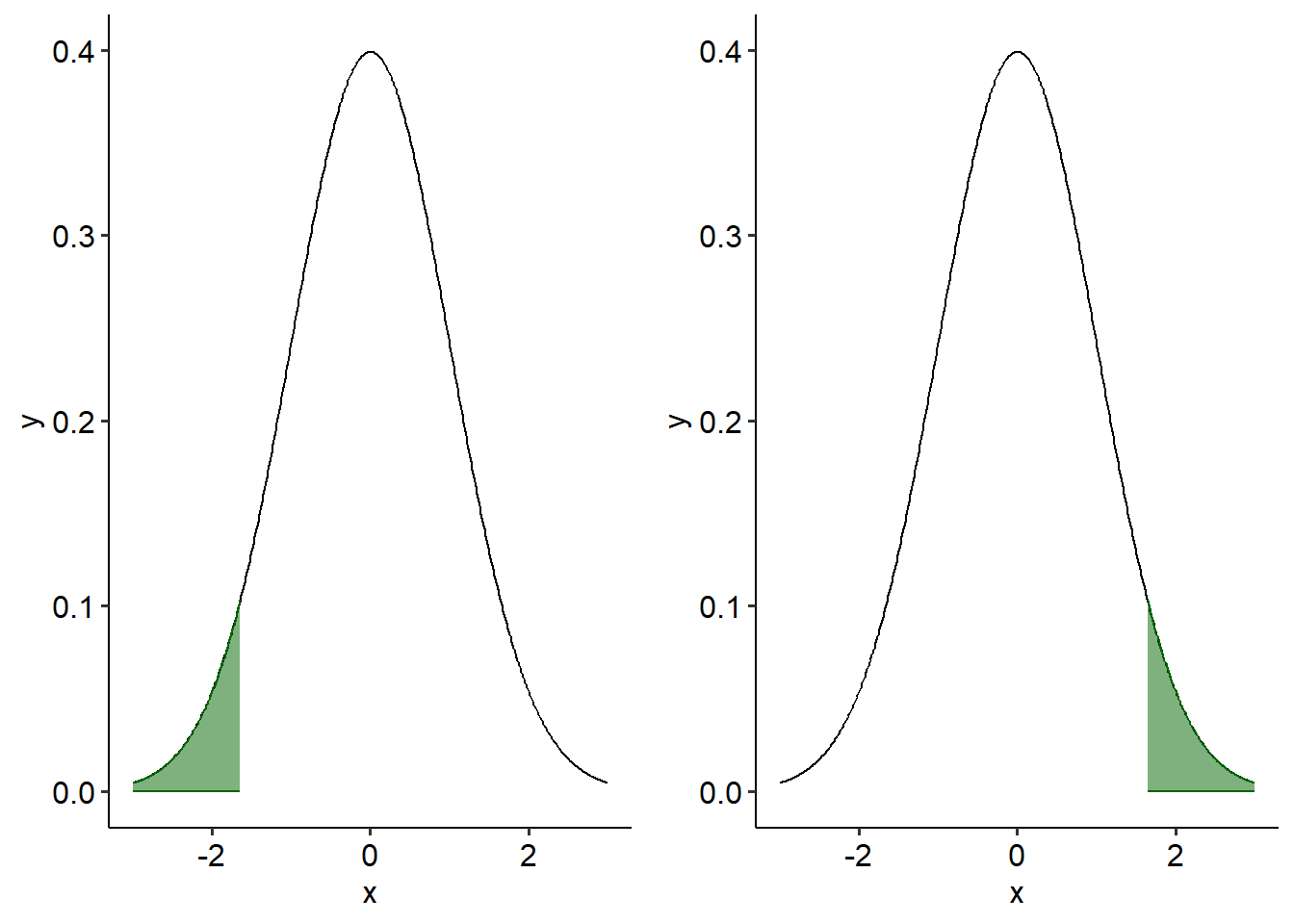
In a one-tailed hypothesis, we predict that the effect exists in a specific direction (hence, they are directional hypotheses). For example, we might predict that Group A is bigger than Group B. Or, we might predict that as X increases, Y increases too.

The two curves below show the significance levels for one-tailed hypotheses. If we predicted that Group A was smaller than Group B, we would only reject the null hypothesis if Group A really was smaller than Group B, and this difference was large enough to be statistically significant (i.e. within one of the green tails).