4.5 Confidence intervals

As we saw on the page about p-values, some people are vocal about their distaste for relying solely on p-values for decision making. One way of augmenting our estimates is to calculate a confidence interval for each estimate we make. Confidence intervals provide an estimate of the precision of our estimate, and so are a crucial concept to know about.

4.5.1 A reminder from the previous module

It’s time to force you to remember what the graph below means once again (I promise this is the last time you will see this figure! I think). By now you should be very familiar with what this graph shows; namely, that 95% of the data in a normal distribution lies within 1.96 standard deviations either side of the mean, yada yada.

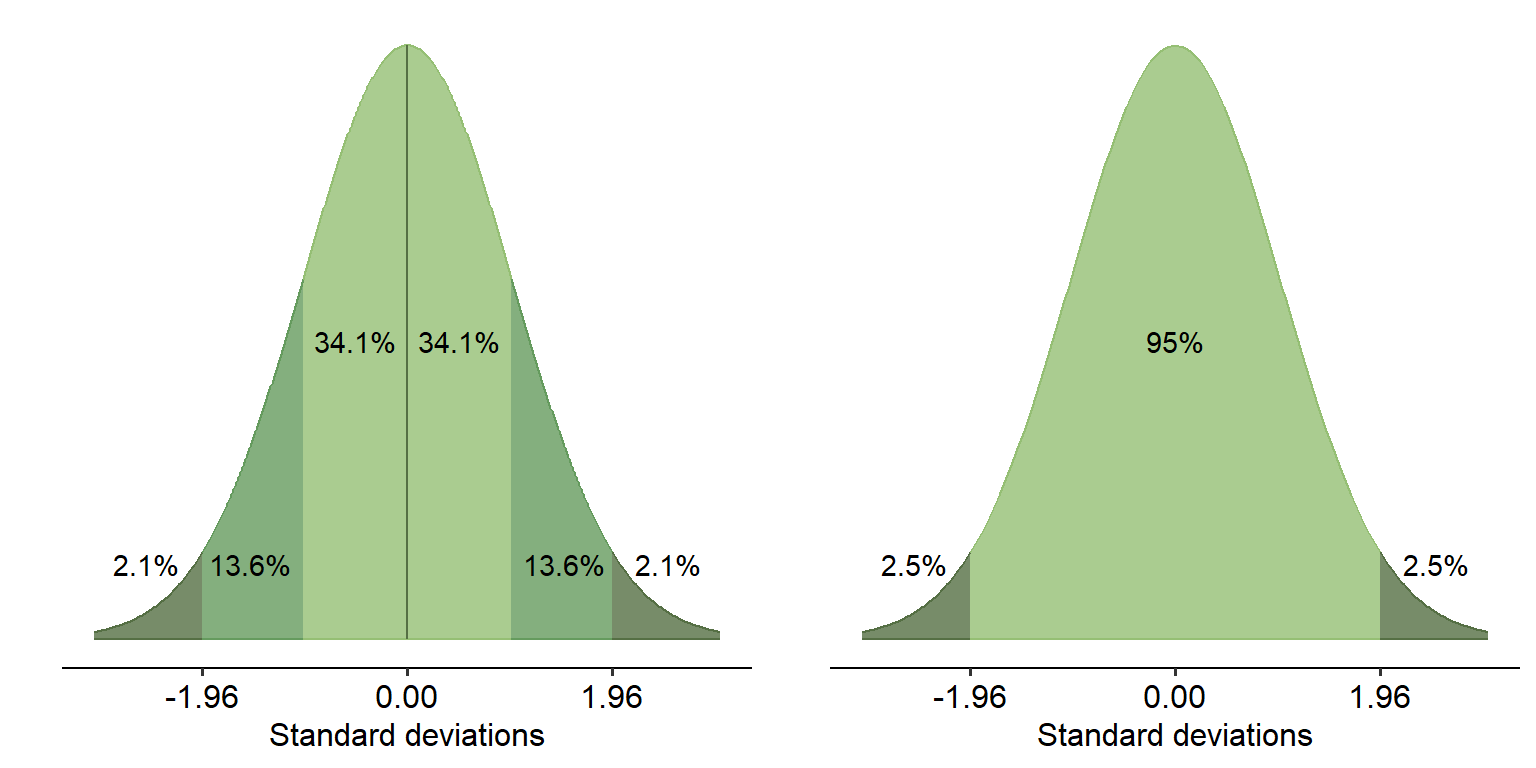
This sounds all well and good, but this provides us with some useful information. If all that business about values within 1.96 standard deviations is still fresh in your mind, this next statement should be a no-brainer: if 95% of our data on a normal distribution lies within 1.96 SD either side of the mean, that means that there is a certain range of values that 95% of our data falls in.

For example, say we have a sample of scores on a test, with a mean of 70 and a standard deviation of 4. If we want to know where 95% of the scores lie in this sample, we would do the following calculation:

\[ 95\% \ range = M \pm (1.96 * SD) \]

Using this formula, we can calculate the values where 95% of the data lie:

\[ 95\% \ range = M \pm (1.96 * SD) \] \[ 70 \pm 7.84 \]

\[ = 62.16, 77.84 \] In other words, 95% of our data in this sample lie between 62.16 and 77.84. The remaining 5% of the sample lie above or below these values.

4.5.2 Confidence intervals

We can use the same principle to make inferences about the true population parameter. When we take a sample, each one will have its own standard error (remember this reflects an estimate of the distance between the sample mean and the true population mean). If we were to repeatedly take samples, in the long run we would expect the true population mean to fall within 95% of all sample means. And, just like the normal distribution, when we look at the sampling distribution of the means below, 95% of all sample means will fall within 1.96 standard errors (thanks to the Central Limit Theorem).

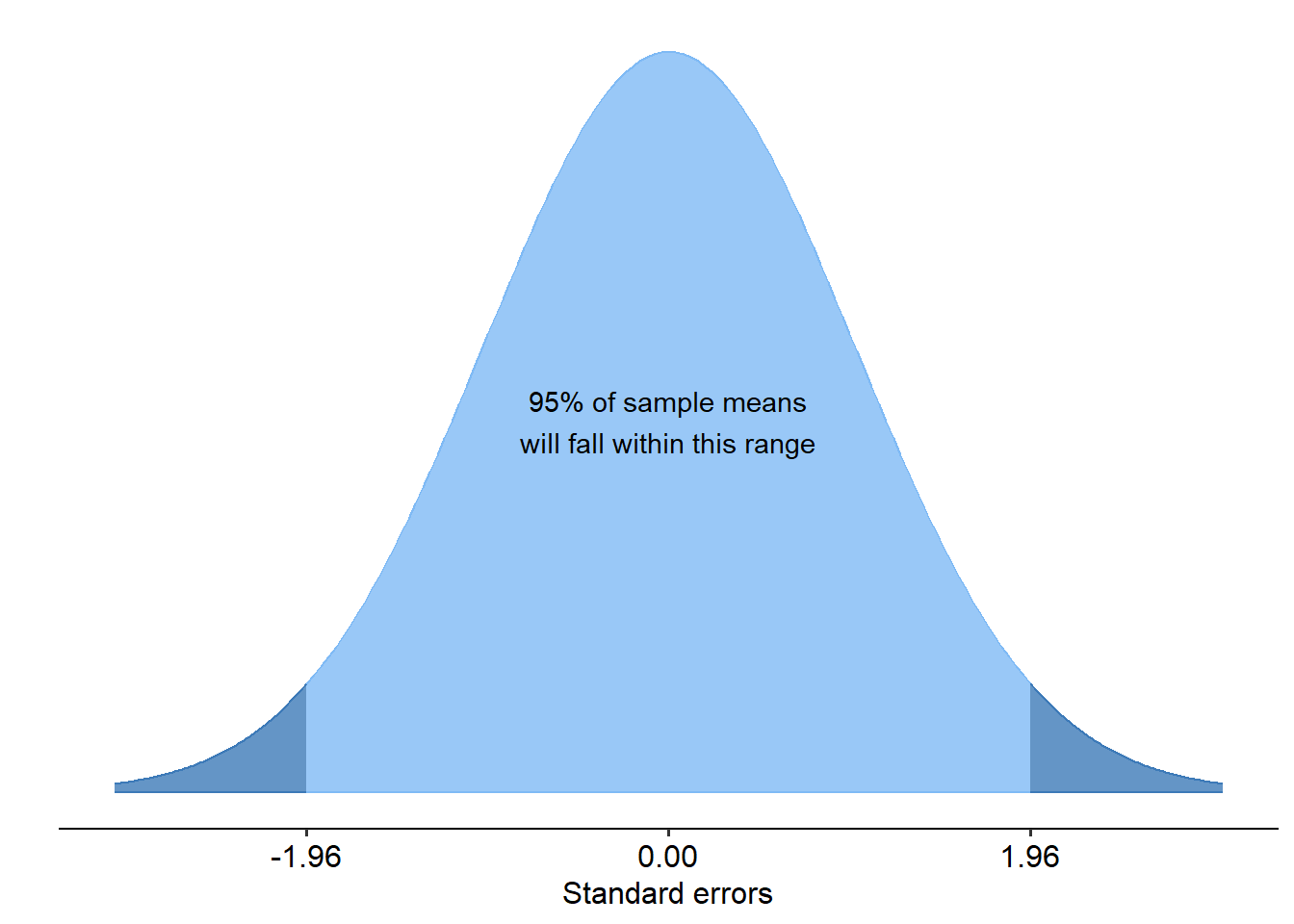
With this important property in mind, we can calculate a 95% confidence interval. This is an estimate of the range of values for our estimate of the parameter. In other words, it is a measure of precision. The formula for a 95% confidence interval, as it turns out, is exactly the same as above with one change:

\[ 95\% CI = M \pm (1.96 \times SE) \]

Therefore, if we have an estimate of a population parameter (e.g. what the population mean is), we can use a 95% CI around that estimate to quantify the precision/uncertainty of that estimate. If a confidence interval is narrow, it suggests our estimate is quite precise.

This can be extremely informative: not only can we use CIs to infer whether an effect is significant or not, but now they quantify how precise our estimates are. For example, pretend that we have a null hypothesis that a parameter is equal to 0 (as is usually the case). If we calculate a confidence interval and that happens to include the value of 0 (e.g. 95% CI: [-0.5, 1.5]), we can immediately infer that 0 is a likely value for this parameter - and thus, the null hypothesis is plausible. On the other hand, if the CI did not include 0 then we could infer that there likely is a significant effect.

Likewise, a CI of something like [0.5, 0.8] compared to a CI of [0.2, 20.5] tells us that the former is a much more precise of a parameter estimate than the latter.

Not all confidence intervals though will contain the true parameter purely because of how samples work (i.e. the inherent error between a sample and a population). In addition, it does not mean that there is a 95% chance a single interval will contain the true parameter. So what does the 95% part refer to?

4.5.3 Confidence

The confidence level is a long-run probability that a group of confidence intervals will contain the true population parameter. A 95% confidence level means that if we were to take samples repeatedly and calculate a CI for each one, 95% of those CIs will contain the true population parameter in the long-run.

Or, say if you were to take 100 samples and calculate a CI for each one, 95 of them would include the true population parameter:

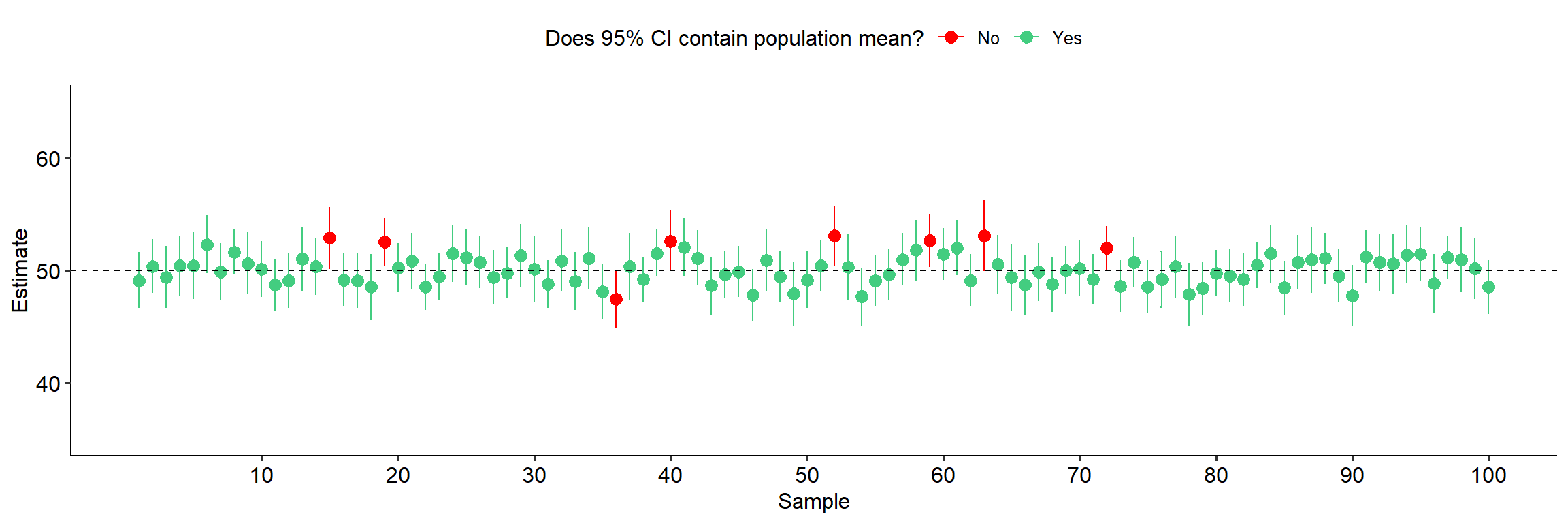
The 95% long-run probability does not change with sample size. What does change, however, is the precision of the estimates. This makes sense if you remember the formula for standard error, which divides by the square root of n. A larger n will lead to lower SE, and thus narrower confidence intervals. Below is an example with a much larger sample size. Notice how the confidence intervals are now much smaller:

The choice of 95% is conventional, like alpha (our significance criterion); we can (but often don’t) change our level of confidence. This changes the relevant formula for calculating the interval, as in the examples below:

\[ 90\% CI = M \pm (1.645 \times SE) \]

\[ 99\% CI = M \pm (2.576 \times SE) \]

Notice that the value we multiply the SE by has changed. If you have been especially observant so far, you may have figured out what these values are: they’re z-scores!

4.5.4 Confidence intervals in literature

On the page about p-values, I left a brief note around some of the current discourse around the usefulness (or uselessness) of p-values. Proponents of getting rid of p-values/moving away from them advocate strongly for two alternatives: a) effect sizes (self-explanatory; we will come to this) and b) confidence intervals, to show the range of long-run plausible values for the estimate.

Again, we won’t be taking an especially strong stance either way. That being said, it is now fairly common practice to report 95% confidence intervals alongside the results of significance tests for transparency. Programs like Jamovi will usually calculate these intervals automatically for you.