8.1 Correlations
We’ve talked a surprising amount about correlations in this subject, but we haven’t considered how to actually test if two things are correlated to begin with. We change that this week with an overview of correlation coefficients.
8.1.1 Correlation coefficients
We can quantify the strength of two variables using a correlation coefficient, which gives us a measure of how tightly these two variables are related.
To start, we need to know what covariance is. Covariance simply describes how two variables change with each other. For instance, if two variables have a positive covariance, this means that as one variable increases, so does the other. Similarly, if two variables have a negative covariance, this means that as one increases the other decreases. See if you can describe what the covariances would be like below:
Correlation coefficients are just another way of describing this. Correlation coefficients have the following properties:
- They are between -1 and +1
- The sign of the correlation describes the direction - a positive value represents a positive correlation
- The numerical value describes the magnitude
- A correlation of 1 means a perfect correlation; a correlation of 0 means a negative correlation
- A rough guideline for this subject, r = .20 is weak, r = .50 is moderate, r = .70 is strong
- Visually, a magnitude of 0 corresponds to a flat line; the steeper the line, the higher the magnitude
There are many types of correlation coefficients, but the most common is the Pearson’s correlation coefficient. It’s calculated using the below (simplified) formula:
\[ r = \frac{Cov_{xy}}{SD_x \times SD_y} \]
In this subject we won’t expect you to calculate a correlation coefficient by hand, but the key takeaway here is that by dividing a value by a standard deviation (or, in this case, a product of two SDs), we are standardising the covariance. Hence, a correlation coefficient is a standardised measure, meaning that we can compare correlation coefficients quite easily across variables regardless of their scale.
8.1.3 Testing correlations in R
Statistical programs like Jamovi and R will allow us to not only quantify a correlation between two variables, but test whether this correlation is significant. Generally, when working with continuous data it never hurts to run a basic correlation.
Here is an example using a simple dataset containing the gender, height and speed (the fastest they had ever driven).
## New names:
## Rows: 1325 Columns: 4
## ── Column specification
## ──────────────────────── Delimiter: "," chr
## (1): gender dbl (3): ...1, speed, height
## ℹ Use `spec()` to retrieve the full column
## specification for this data. ℹ Specify the
## column types or set `show_col_types = FALSE` to
## quiet this message.
## • `` -> `...1`Let’s correlate height and speed. This can easily be done in R by using the cor.test() function. You simply need to give it the names of the two columns you want to correlate. By default, this function will run a Pearson’s correlation.
##
## Pearson's product-moment correlation
##
## data: w10_speed$height and w10_speed$speed
## t = 9.2871, df = 1300, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.1977889 0.2997013
## sample estimates:
## cor
## 0.2494356We can see that our correlation is r = .249, which is a relatively weak to moderate correlation. This correlation is also significant (p < .001). We also get a confidence interval around the size of the correlation, which is great for showing the range of possible values. So we might write this up as something like:
There was a significant weak positive correlation between students’ heights and their fastest ever driving speed (r(1300) = .25, p < .001; 95% CI [.20, .30]).
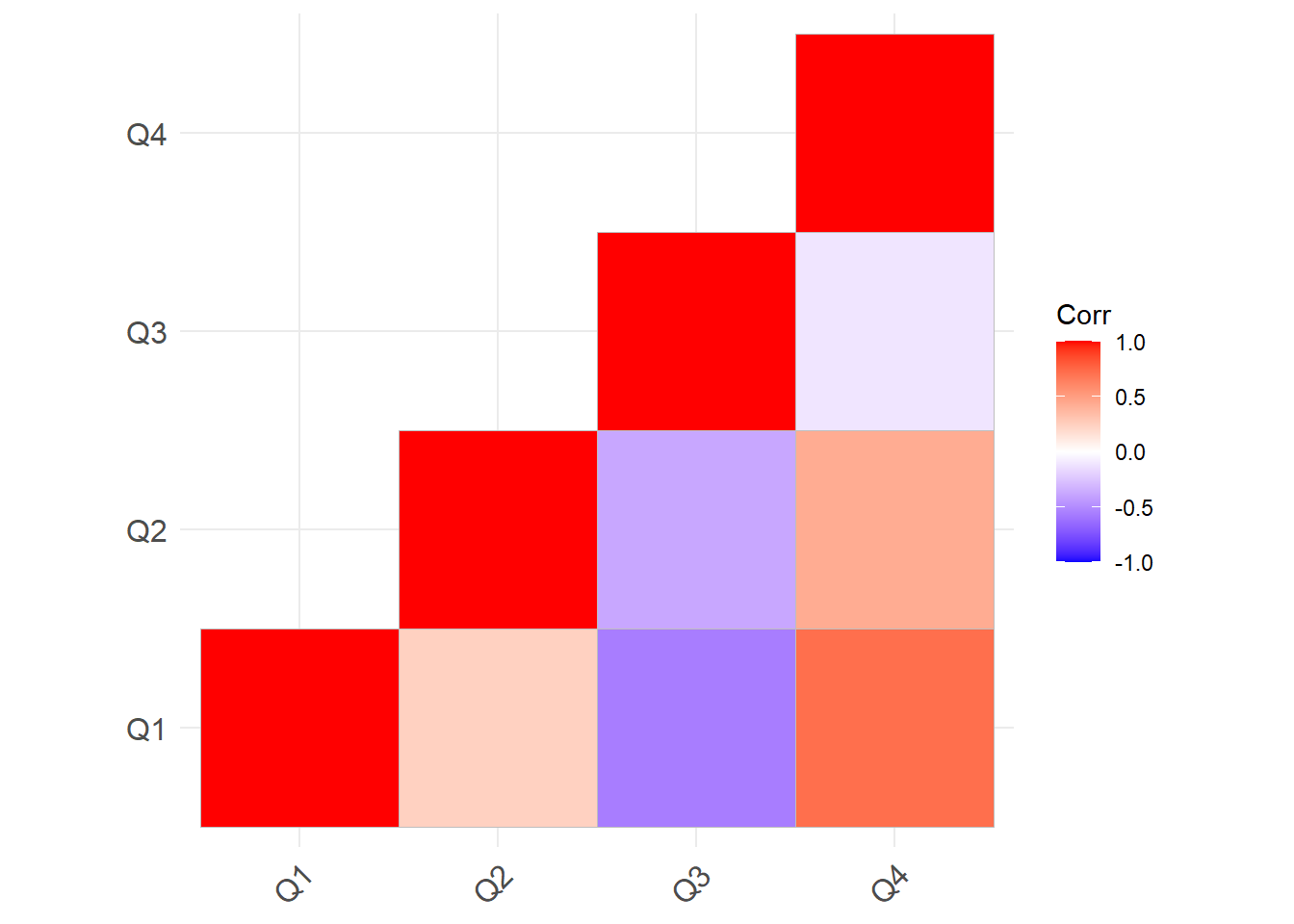
If you need to run multiple correlations at once, there are two ways to visualise them. Below are two types, using fictional questionnaire data.
The first is simply a table, like below:
| Q1 | Q2 | Q3 | Q4 | |
|---|---|---|---|---|
| Q1 | 1.00 | 0.24 | -0.56 | 0.72 |
| Q2 | 0.24 | 1.00 | -0.38 | 0.43 |
| Q3 | -0.56 | -0.38 | 1.00 | -0.11 |
| Q4 | 0.72 | 0.43 | -0.11 | 1.00 |
The second is a correlation heatmap, which is especially effective with many correlations at once (common when working with huge questionnaires or neuroimaging). As shown by the legend on the right, the colour and shade of each square are determined by the strength of the correlation. This can be easily done by the `ggcorrplot package, if you have a correlation matrix formatted in R: