8.6 Predictions
A significant result from a linear regression tells us that our IV significantly predicts our outcome. We can actually use the results of the regression to make predictions about our outcome. This can be really useful in a number of contexts.
8.6.1 Revisiting the linear regression equation
Let’s come back to the equation for a linear regression:
\[ y = \beta_0 + \beta_1x + \epsilon_i \]
The results from the linear regression on the previous page allow us to construct a line of best fit. Using this line of best fit, we can make predictions about a participant’s score on the dependent variable, given their score on the independent/predictor variable.
8.6.2 Building a regression equation
Here’s the coefficient table from the previous page:
##
## Call:
## lm(formula = GoldMSI ~ years_training, data = w10_goldmsi)
##
## Residuals:
## Min 1Q Median 3Q Max
## -35.617 -9.227 2.025 9.773 33.666
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 53.901 5.233 10.300 8.33e-16 ***
## years_training 4.858 1.138 4.271 5.86e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 14.61 on 72 degrees of freedom
## Multiple R-squared: 0.2021, Adjusted R-squared: 0.191
## F-statistic: 18.24 on 1 and 72 DF, p-value: 5.859e-05This table tells us the following things:
- The value of the intercept, \(\beta_0\), is 53.901
- The value of the slope, \(\beta_1\), is 4.858
Now we can make our equation as such:
\[ GoldMSI = 53.901 + (4.858 \times Years) \]
We can now use this to predict scores!
8.6.3 An example prediction
Participant 47, highlighted in green below, has 5 years of musical training. What would their predicted Gold-MSI score to be?
## `geom_smooth()` using formula = 'y ~ x'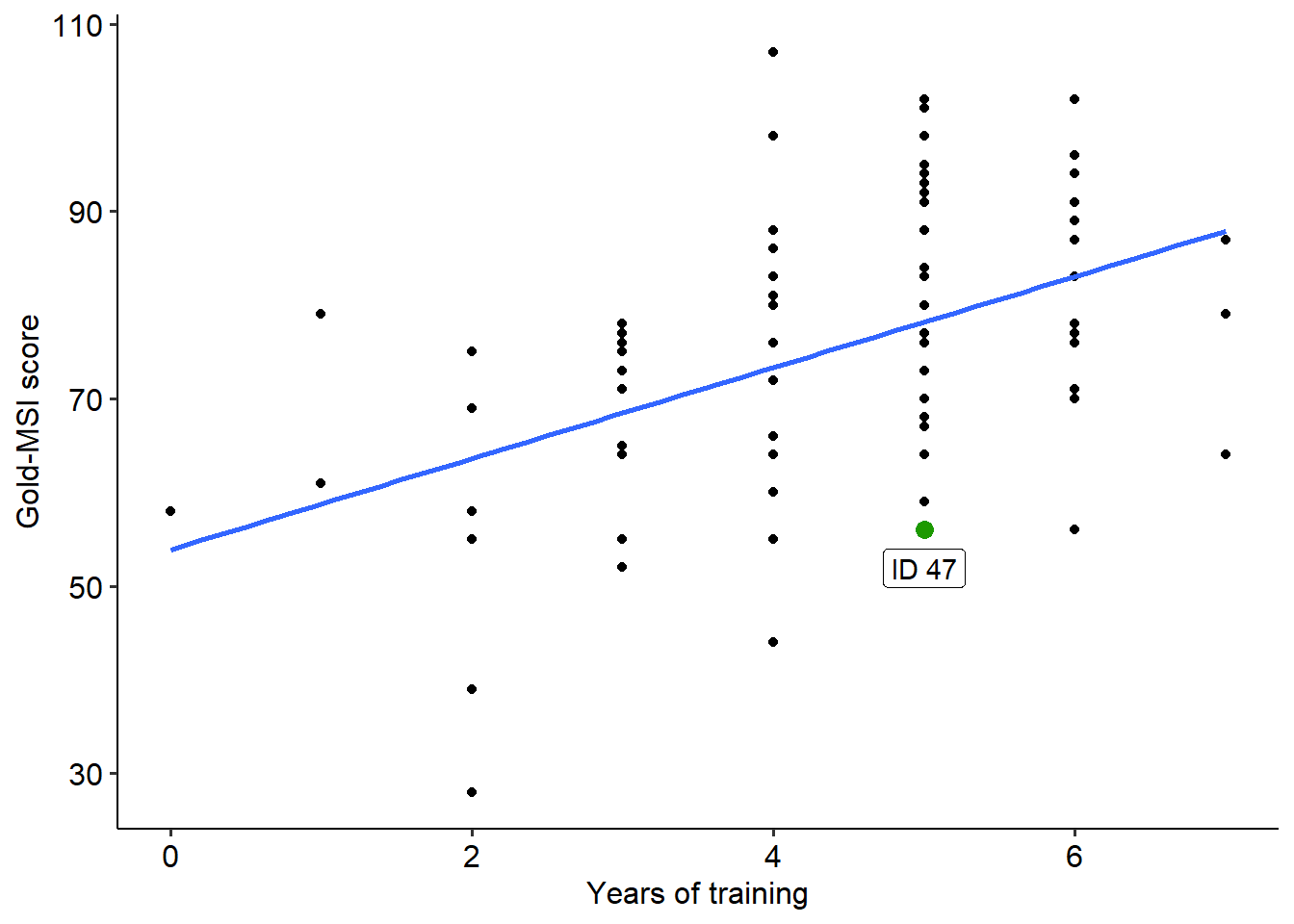
We can use the equation we just built to calculate a predicted score:
\[GoldMSI = 53.901 + (4.858 \times Years)\] \[GoldMSI = 53.901 + (4.858 \times 5)\] \[=78.191\]
Therefore, we would predict someone with 5 years of musical training to have a Gold-MSI score of 78.191. This is where the line sits. Notice however, that the predicted value is noticeably different to the participant’s actual value (which in this instance is 56). The difference between the predicted and the actual value is called the residual - precisely the same residual that we aim to minimise when we fit a regression line to begin with (as well as the same residuals we do assumption tests on).
8.6.4 A warning
While these predictions can be useful, there are two warnings that should be kept in mind.
- Extrapolation is dangerous. While we might get data that appears linear, there is nothing to say that this data will remain linear outside of the bounds of our data. Extrapolating data refers to making inferences beyond the available range, and should be avoided.
- Don’t forget that some data have logical boundaries. For example, the Gold-MSI’s maximum possible score is 126 across all scales. Any preditions that are higher than this are therefore quite easily nonsensical.